| XCorr |
|---|
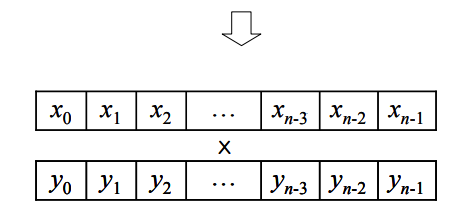
길이가 동일한 수열 \(X=(x_0, x_1, \cdots, x_{n-1})\) 와 \(Y=(y_0, y_1, \cdots, y_{y-1})\)가 있다. 이 두 수열의 각 원소는 음이 아닌 정수이다. 다음은 \(n=5\)인 경우의 한 예이다. \(X=(1,0,0,0,1)\) \(Y=(0,5,2,0,1)\) 임의의 정수 \(t\)가 주어졌을 때 \(XCorr(t)\)는 다음과 같이 정의된다. \(XCorr(t)=\displaystyle\sum_{i=0}^{n-1}{x_iy_{i+t}}\) (\(i<0\)이거나 \(i\geq n\)이면 \(x_i=y_i=0\)으로 간주한다.) 예를 들어 \(t\)가 \(0, 1, -1\)일 때, \(XCorr(t)\) 값은 다음과 같이 계산된다. \(XCorr(0) = x_0y_0 + x_1y_1 + \dots + x_{n-1}y_{n-1}\)
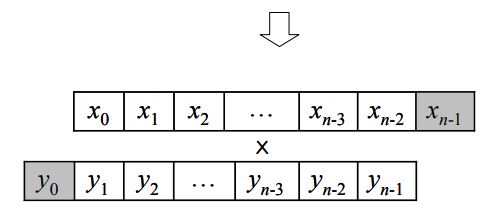
\(XCorr(1) = x_0y_1 + x_1y_2 + \dots + x_{n-1}y_n\)
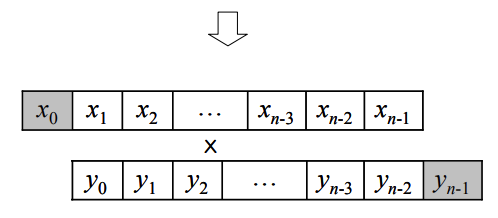
회색 칸에 들어있는 부분은 계산결과에 영향을 주지 않음에 주의하라. \(y_0\)는 계산식에 포함되지 않고, \(x_{n-1}\)은 곱해지는 \(y_n=0\) 이므로 계산 결과에 영향을 주지 않는다. 따라서 예시 수열 \(X\)와 \(Y\)에서 \(XCorr(1)\)은 다음과 같이 계산할 수 있다. \(1\times5+0\times2+0\times0+0\times1=5\) \(XCorr(-1) = x_0y_-1 + x_1y_0 + \dots + x_{n-1}y_{n-2}\)
임의의 \(t\)값의 범위 \((a \le t \le b)\)에 대해 \(XCorr(t)\)를 모두 구해서 더한 값 \(S(a,b)\)는 다음과 같이 정의된다. \(S(a,b)=\displaystyle\sum_{a \le t \le b}{XCorr(t)}\) 수열 \(X, Y\)와 \(t\)의 범위 \(a, b\)가 주어졌을 때 \(S(a,b)\)를 구하는 프로그램을 작성하시오. |
| 입력 | |
|---|---|
다음 정보가 입력으로 주어진다. 첫 번째 줄에는 수열 \(X\)에서 \(0\)이 아닌 정수의 개수 \(N\)이 주어진다.(수열의 길이 \(n\)이 아님). 다음 \(N\)개의 줄에는 수열 \(X\)의 각 양의 정수 \(x_i\)에 대해 인덱스 \(i\) 와\( x_i\)값이 인덱스의 오름차순으로 주어진다. 다음 줄부터는 수열 \(Y\)가 \(X\)와 동일한 방식으로 주어진다. (\(Y\)에서 \(0\)이 아닌 정수의 개수 \(M\)이 주어지고 다음 \(M\)개의 줄에는 수열 \(Y\)의 각 양의 정수 \( y_i\)에 대해 인덱스 \(i\)와 \(y_i\) 값이 인덱스의 오름차순으로 주어진다.) 다음 줄에는 \(t\)의 범위의 최솟값인 정수 \(a\)가 주어지고, 그 다음 줄에는 \(t\)의 범위의 최댓값인 정수 \(b(a \le b)\)가 주어진다.
< 부분문제의 제약 조건 > 모든 부분 문제에서 입력으로 주는\(x_i, y_i\)는 \(1 \leq x_i, y_i \leq 3,000\)이다.
| |
| 출력 | |
|---|---|
\(S(a,b)=\displaystyle\sum_{a \leq t \leq b}{XCorr(t)}\)값을 정수로 출력하라. | |
| 예시 | |||
|---|---|---|---|
| 1 | 입력 | 3 0 1 1 1 2 1 3 0 1 1 2 2 3 -1 1 | |
| 출력 | 14 | ||
| 2 | 입력 | 3 0 1 4 4 9 5 3 1 3 2 7 10 7 -2 2 | |
| 출력 | 73 | ||
| 출처 | |
|---|---|
| 2018년 한국정보올림피아드 전국 본선 고등부 2번 | |