| 화살표 그리기 |
|---|
직선위에 위치를 나타내는 0, 1, 2, .... 아 같은 음수가 아닌 정수들이 일정한 간격으로 오른쪽방향으로 놓여 있다. 이러한 위치들 중 N개의 위치에 하나씩 점들이 주어진다(<그림 1>). 주어진 점들의 위치는 모두 다르다. 두 점 사이의 거리는 두 점의 위치를 나타내는 수들의 차이이다. 
각 점은 N개의 색깔 중 하나를 가진다. 편의상, 색깔은 1부터 N까지의 수로 표시한다. 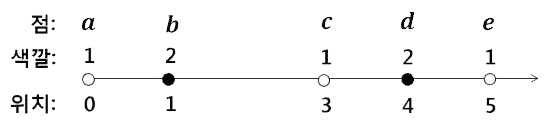
위의 조건으로 화살표를 그리면, 아래 <그림 3>과 같이 점 a의 화살표는 c로 연결된다. 점 b와 d의 화살표는 각각 d와 b로 연결된다. 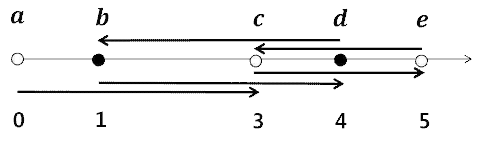
점들의 위치와 색깔이 주어질 때, 모든점에서 시작하는 화살표들의 길이 합을 출력하는 프로그램을 작성하시오. |
| 입력 | |
|---|---|
첫 번째 줄에는 점들의 개수를 나타내는 정수 N이 주어진다. 다음 N개의 줄 각각에는 점의 좌표와 색깔을 나타내는 두 정수 x와 y가 주어진다.
< 부분문제의 제약 조건 > 모든 부분문제에서 점들의 위치 x와 색깔 y는 각각 0≤x≤105, 1≤y≤N를 만족한다.
| |
| 출력 | |
|---|---|
모든 점에서 시작하는 화살표들의 길이 합을 출력한다. | |
| 예시 | |||
|---|---|---|---|
| 1 | 입력 | 5 0 1 1 2 3 1 4 2 5 1 | |
| 출력 | 13 | ||
| 2 | 입력 | 7 6 1 7 2 9 1 10 2 0 1 3 1 4 1 | |
| 출력 | 16 | ||
| 출처 | |
|---|---|
| 2018년 한국정보올림피아드 전국 본선 초등부 2번 | |
